- S->S+A | S-A | A+S | A-S | B*A
B->aB | B(a+b) | B*a | a(a+b) |b
A -> a
Jawab
S->S+A | S-A | A+S | A-S | B*A
Left recursive
S-> A+SS’ | A-SS’ | B*AS’
S’->+AS’ | -AS’ | ε
Left factoring
S-> AS” | B*AS’
S’->+AS’ | -AS’ | ε
S”-> +SS’ | -SS’
B->aB | B(a+b) | B*a | a(a+b) |b
Left recursive
B->aBB’ | a(a+b)B’ |bB’
B’-> (a+b)B’ | *aB’ | ε
Left factoring
B-> aB” |bB’
B’-> (a+b)B’ | *aB’ | ε
B”-> BB’ | (a+b)B’
Sehingga hasil penyederhanaan
S-> AS” | B*AS’
S’->+AS’ | -AS’ | ε
S”-> +SS’ | -SS’
B-> aB” |bB’
B’-> (a+b)B’ | *aB’ | ε
B”-> BB’ | (a+b)B’
A -> a
Menentukan First dan Follow
First (S) = {a,b}
First (S’) = {+,-, ε }
First (S”) = {+,-}
First (B) = {a,b}
First (B’) = { (,*, ε }
First (B”) = {a,b,( }
First (A) = {a}
Follow(S)={$}
Follow(S)={$}
Follow(S)={$}
Follow(B)={*}
Follow(B)={*}
Follow(B)={*}
Follow(A)={+,-,$}
2. Soal:
S -> if E then S | if E then S else S | V:= E
V -> id | id [E]
E -> E+T | E-T | T
T -> T*F | T/ F| F
F -> V | (E) | const
Jawaban
S -> if E then S S’| V:= E
S’ -> ε | else S
V -> id V’
V’ -> ε | [E]
E -> TE’
E’ -> +TE’ | -TE’ | ε
T -> FT’
T’ -> *FT’ | / FT’| ε
F -> V | (E) | const
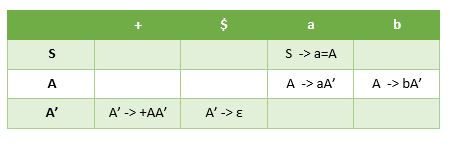
3. Dari CFG (Context Free Grammar) berikut ini :
S -> a=A
A -> aA’ | bA’
A’ -> +AA’ | ε
First (S) = { a } Follow (S) = { $ }
First (A) = { a,b } Follow (A) = { $,+ }
First (A’) = { +, ε } Follow (A’) = { $,+ }
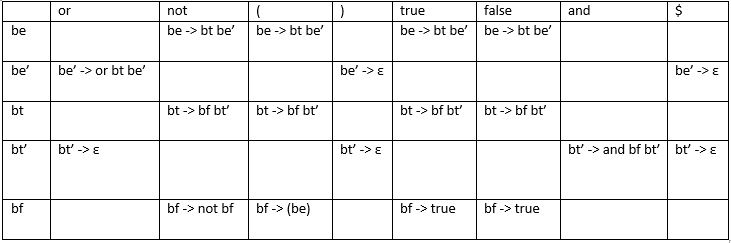
4. Soal
be -> bt be’
be’ -> or bt be’
be’ -> ε
bt -> bf bt’
bt’ -> and bf bt’
bt’ -> ε
bf -> not bf
bf -> (be)
bf -> true
bf -> false
periksa input not ( true or false ) and true and false not (false) true
jawab
first (be) = {not , ( , true, false}
first (be’) = {or , ε}
first(bt) = {not, (, true,false}
first(bt’)= {and, ε}
first(bf)= {not, (, true, false}
follow (be) = {$, ) }
follow (be’) = {$ , ) }
follow(bt) = {or, $, ) }
follow(bt’)= {or, $, ) }
follow(bf)= {or, $, ), and }
Kelompok 5
Bernardus Robby 1501144332
Elisabeth Oktaviani 1501154516
I Kadek Mega Adi Utama 1501159170
Michael Chandra 1501146621